はじめに
ビルディングパズルでは、高さが 1 から 4 のビルを上から見ていると考えます。
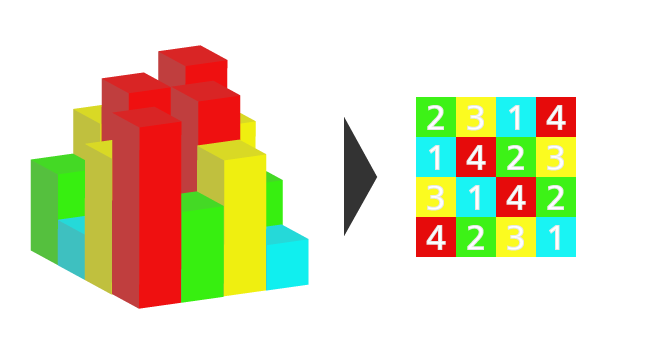
ビルディングパズルは、はじめにあたえられたヒントを手がかりにしてルールをやぶらないようにビルのはいちを決めるパズルゲームです。
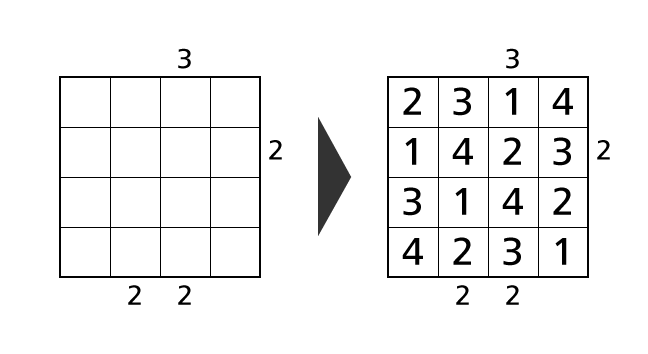
ビルディングパズルをはじめてあそぶ人のために、ここでは 4×4 のサイズのビルディングパズルについてルールの説明をくわしくします。そのあと、じっさいに例題をといてみます。
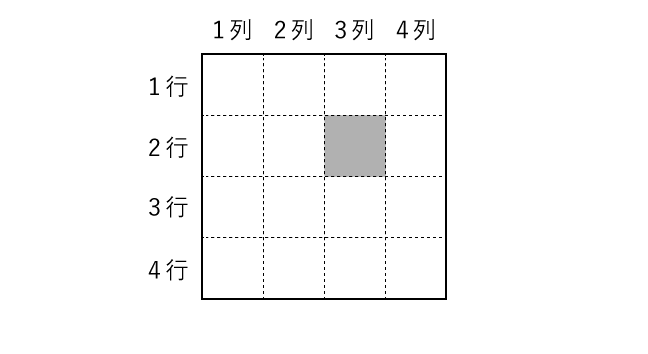
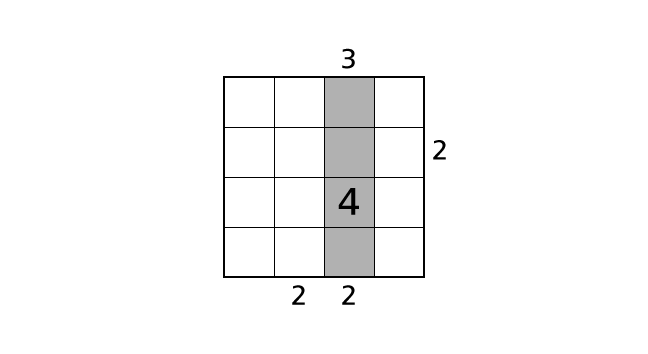
説明では、パズルの数字を入れるハコのよこのならびを 行(ぎょう)、たてのならびを 列(れつ) とよびます。それぞれのハコを行と列のばんごうをつかって、ハコ (1,1) のようによびます。例えば次のパズルの色がついているハコは、ハコ (2,3) とよびます。
ルール
ビルディングパズルのルールは次の 3 つです。ルールをしっかりおぼえて、ルールをやぶっていないか注意しながら数字のはいちを決めましょう。
- それぞれの行には 1 から 4 の数字がそれぞれ 1 度ずつ入ります。
- それぞれの列には 1 から 4 の数字がそれぞれ 1 度ずつ入ります。
- 枠の外の数字はその方向から見えるビルの数を表しています。
上のパズルを例題として、それぞれのルールについてくわしく見ていきましょう。
ルール 1
それぞれの行には 1 から 4 の数字がそれぞれ 1 度ずつ入ります。つまり、ひとつの行に同じ数字が 2 回でてくることはありません。例題のパズルではヒントからハコ (3,3) は 4 しか入れることができないハコ であることがわかります。するとルール 1 より 3 行目にはハコ (3,3) 以外に 4 が出てくることはありません。
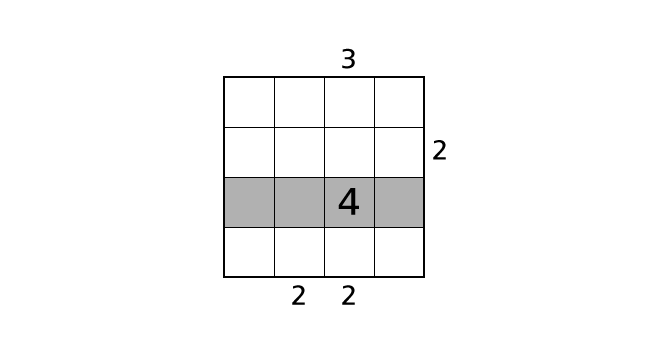
このことを他の数字のはいちを決める時のヒントとしてつかうことができます。
ルール 2
それぞれの列には 1 から 4 の数字がそれぞれ 1 度ずつ入ります。つまり、ひとつの列に同じ数字が 2 回でてくることはありません。例題のパズルでは、3 列目にはハコ (3,3) 以外に 4 が出てくることはありません。
ルール 3
枠の外の数字はその方向から見えるビルの数を表しています。ビルディングパズルでは、このヒントとルール 1 とルール 2 から数字のはいちを決めていきます。
高いビルは後ろにある低いビルをかくしてしまいます。たとえば、4 3 2 1 のじゅんでならんでいるビルは、左から見ると 1 つのビルだけがみえて、右から見ると 4 つのビルがみえます。
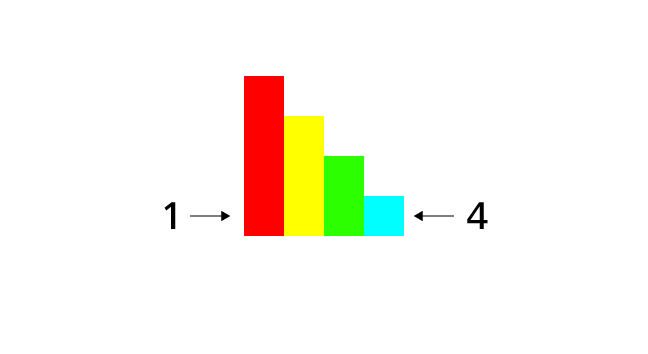
4 つのビルがみえている場合は、その方向から見たビルのならびじゅんは 1 2 3 4 のじゅんばんに決まります。それ以外のならびじゅんでは 4 つのビルがみえることはないからです。
1 つのビルだけがみえている場合には、一番手前に高さ 4 のビルがあることがわかります。しかし、その後ろのビルのじゅんばんは、次の 6 つの場合があって決めることができません。
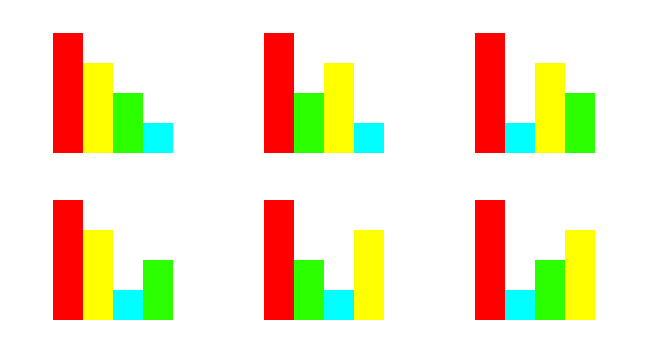
このような場合は、他のヒントやルールをつかって数字のはいちを決めます。
とき方
ここでは、じっさいに次の例題をといてみます。ただし、とき方はひとつだけではありません。他のとき方も見つけてみましょう。
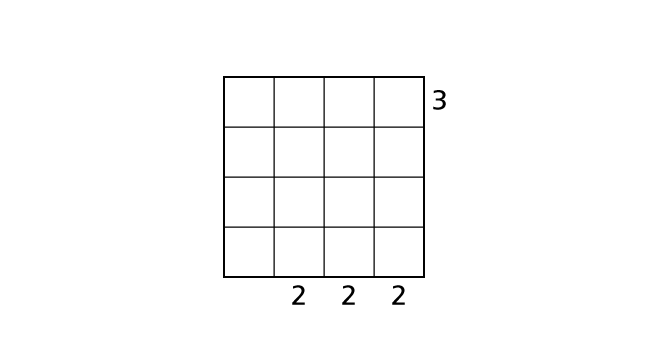
手順 1
ビルディングパズルをとくコツは、4 のはいちから考えることです。
4 行目に注目しましょう。ルール 1 より 4 行目には 4 が 1 度だけ出てきます。また、4 が一番手前にあるとその方向からみえるビルの数は 1 になります。この 2 つのことから、ハコ (4,1) は 4 しか入れることができないハコ であることがわかります。
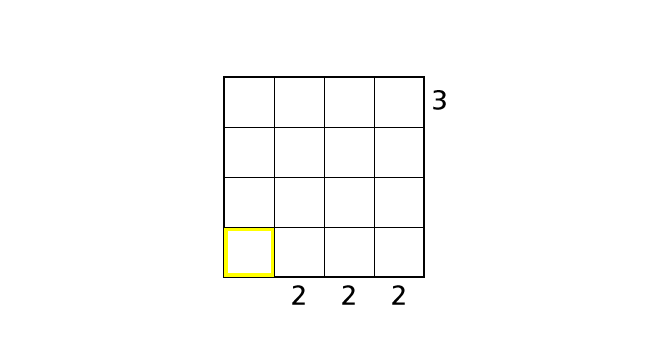
ハコ (4,2)、ハコ (4,3)、ハコ (4,4) に 4 が入るとすると、下から見ると 2 つのビルがみえるというルール 3 をやぶってしまいます。数字をはいちしましょう。
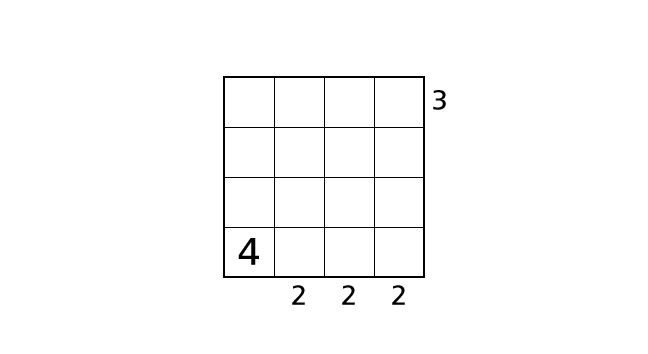
手順 2
引き続き、4 のはいちについて考えます。次は、1 行目に注目しましょう。ハコ (4,1) に 4 を入れたので、ルール 2 より、ハコ (1,1) には 4 を入れることはできません。
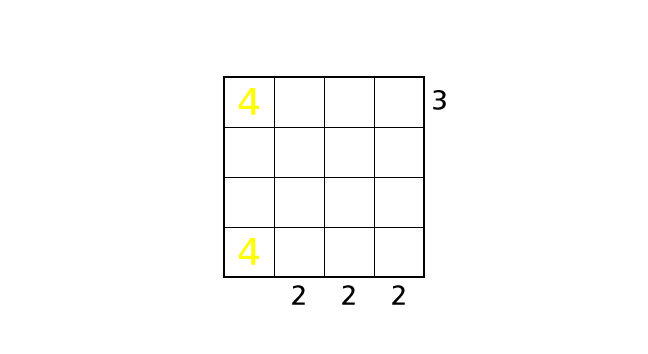
それ以外の場合について、場合分けをして考えます。ハコ (1,3) とハコ (1,4) に 4 を入れる場合を考えます。
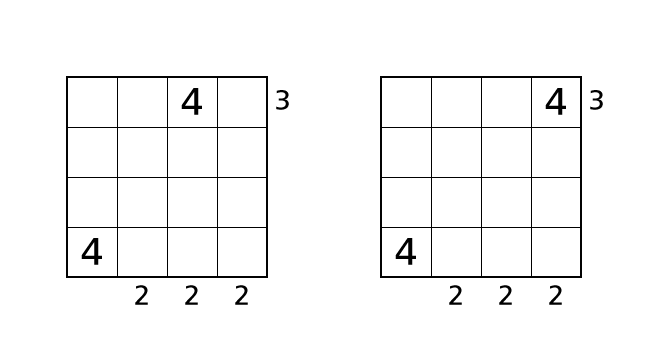
この場合はどちらも右から見えるビルの数が 3 になることはありません。つまりルール 3 をやぶってしまいます。このことから、ハコ (1,2) が 4 しか入れることができないハコ であることがわかります。数字をはいちしましょう。
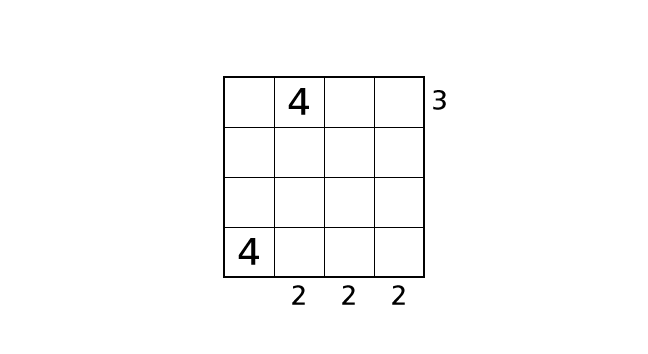
手順 3
4 のはいちはこれ以上決めることができないので、次は 3 のはいちについて考えます。2 列目に注目しましょう。ハコ (1,2) には 4 を入れたので、3 を入れることができるハコは、ハコ (2,2)、ハコ (3,2)、ハコ (4,2) の 3 つです。
場合分けをして考えます。ハコ (2,2) とハコ (3,2) に 3 を入れる場合を考えます。
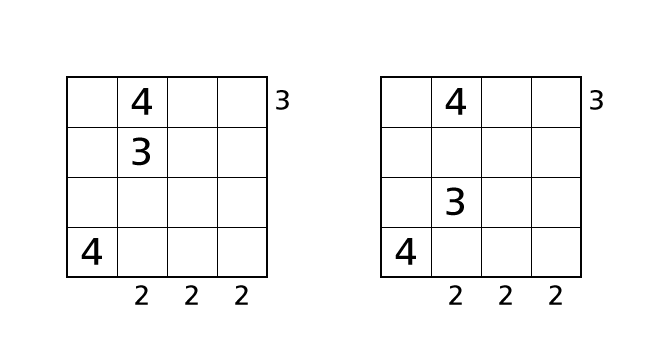
この場合は他の数字をどのようにはいちしても、下から見えるビルの数は 2 より大きくなります。これは下から見えるビルの数が 2 であるというルール 3 をやぶってしまいます。ハコ (2,2)、ハコ (3,2) には 3 を入れることができないので、ハコ (4,2) が 3 しか入れることができないハコ であることがわかります。数字をはいちしましょう。
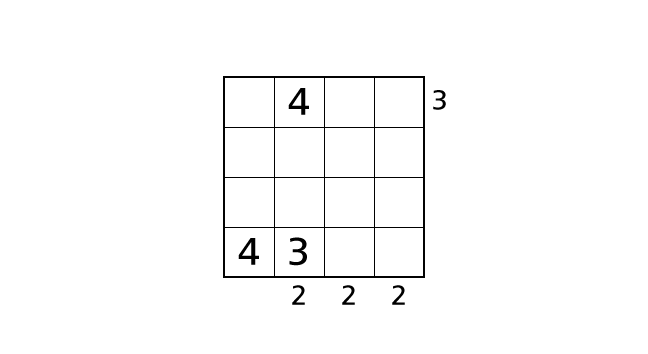
手順 4
3 のはいちについてもこれ以上決めることはできないので、4 のはいちについて場合分けをして考えます。ルール 1 とルール 2 をやぶらないように 4 をはいちすると次の 2 つの場合が考えられます。
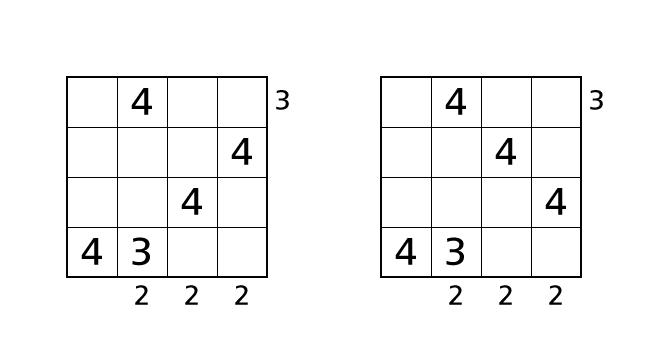
1 つめの場合について考えます。4 列目に注目しましょう。3 を入れることができるハコは、ハコ (1,4)、ハコ (3,4)、ハコ (4,4) の 3 つです。場合分けをして考えます。
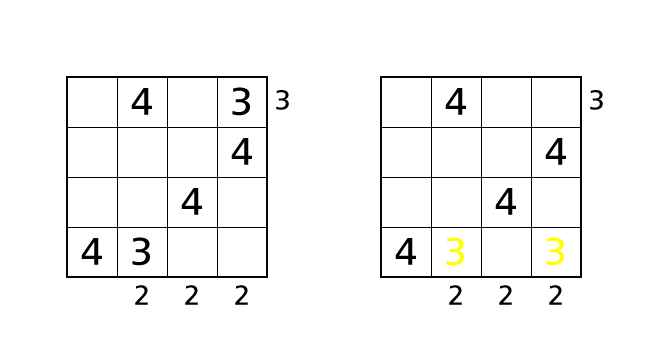
ハコ (1,4) に 3 を入れる場合は、1 行目の右から見えるビルの数は 2 になるので、ルール 3 をやぶってしまいます。ハコ (4,4) に 3 を入れると、4 行目には 3 が 2 回出てくるので、ルール 1 をやぶってしまいます。最後に、ハコ (3,4) に 3 を入れる場合を考えましょう。
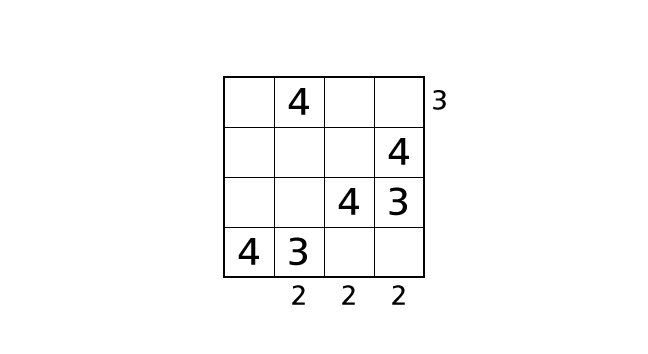
しかし、この場合も問題があります。4 列目は他の数字をどのようにはいちしても、下から見えるビルの数は 3 になるので、ルール 3 をやぶってしまいます。
4 列目にはどのように 3 をはいちしてもルールをやぶってしまうことがわかりました。このようなことがおきたのは 4 のはいちをする時の場合分けでまちがった場合を選んでしまったからです。このあとは、もう一つの場合について考えていきましょう。
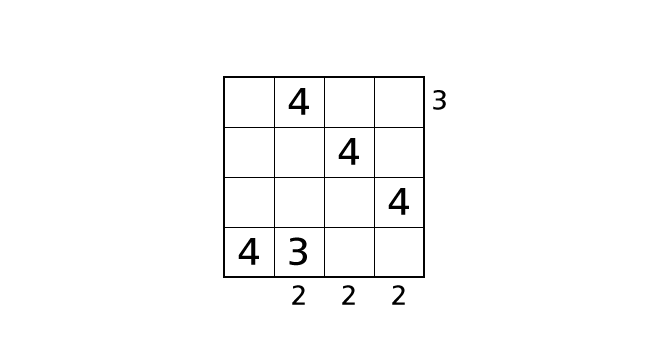
手順 5
4 列目に注目しましょう。3 を入れることができるハコは、ハコ (1,4)、ハコ (2,4)、ハコ (4,4) の 3 つです。場合分けをして考えます。
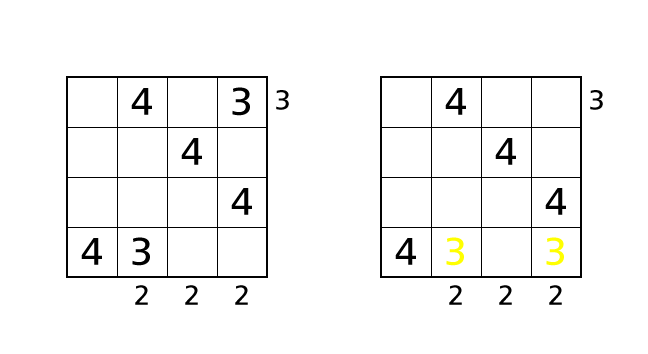
ハコ (1,4) に 3 を入れる場合は、1 行目に残りの数字をどのようにはいちしても右から見えるビルの数は 2 となるのでルール 3 をやぶってしまいます。ハコ (4,4) に 3 を入れると、4 行目に 3 が 2 回出てくるので、ルール 1 をやぶってしまいます。つまりハコ (2,4) が 3 しか入れることができないハコ であることがわかります。
数字をはいちしましょう。
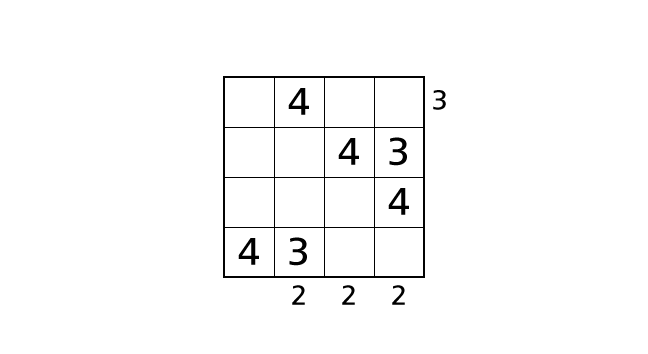
手順 6
3 列目に注目しましょう。3 を入れることができるハコは、ハコ (1,3)、ハコ (3,3)、ハコ (4,3) の 3 つです。場合分けをして考えます。
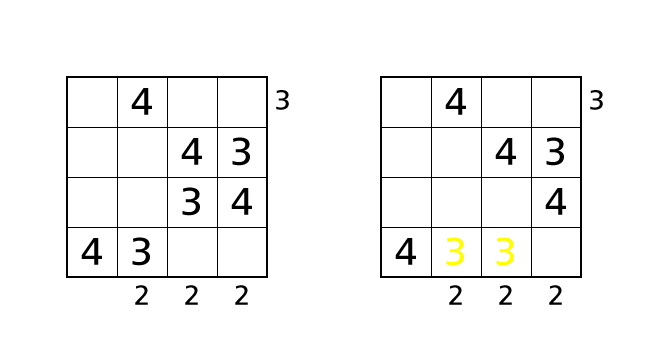
ハコ (3,3) に 3 を入れる場合は、他の数字をどのようにはいちしても下から見えるビルの数は 3 となるのでルール 3 をやぶってしまいます。ハコ (4,3) に 3 を入れると、4 行目に 3 が 2 回出てくるのでルール 1 をやぶってしまいます。つまりハコ (1,3) が 3 しか入れることができないハコ であることがわかります。
数字をはいちしましょう。
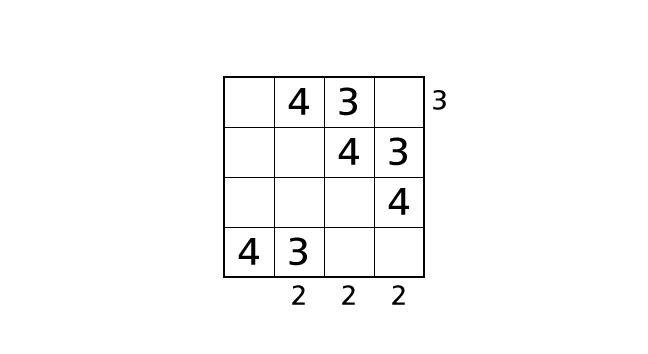
手順 7
1 列目に注目しましょう。3 を入れることができるハコは、ハコ (1,1)、ハコ (2,1)、ハコ (3,1) の 3 つです。場合分けをして考えます。
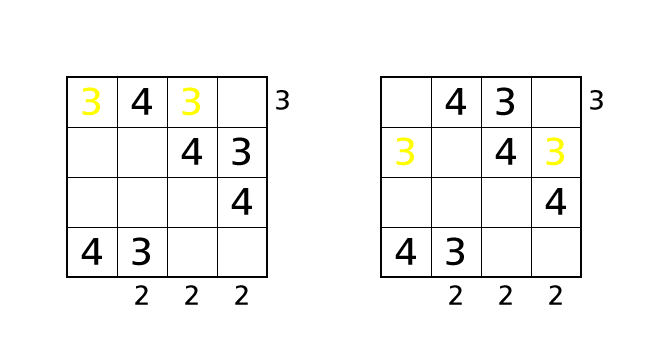
ハコ (1,1)、ハコ (2,1) に 3 を入れた場合は、どちらの場合もルール 1 をやぶってしまいます。つまりハコ (3,1) が 3 しか入れることができないハコ であることがわかります。
数字をはいちしましょう。
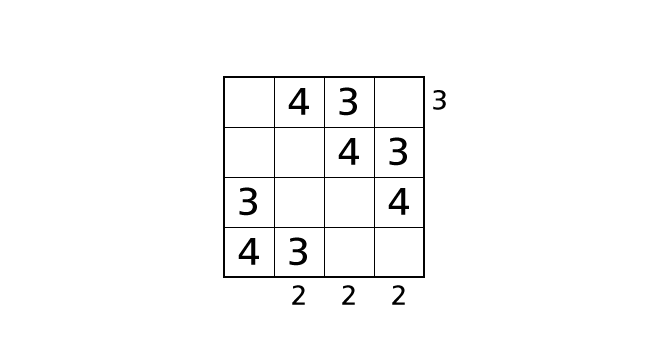
これで 3 と 4 のはいちはすべて終わりました。これからは 1 と 2 のはいちについてヒントをつかって考えていきましょう。
手順 8
3 列目に注目しましょう。1 と 2 のはいちについて場合分けをして考えます。
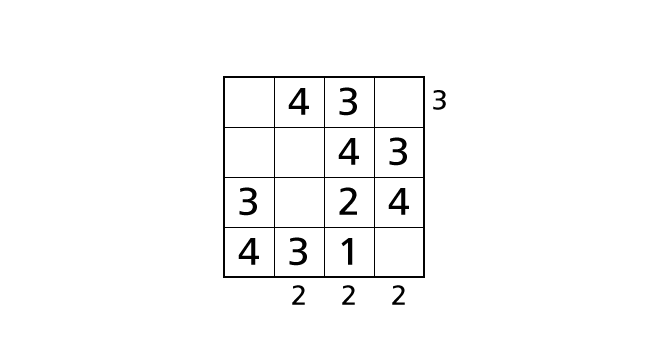
ハコ (3,3) に 2、ハコ (4,3) に 1 を入れる場合は下から見えるビルの数が 3 となるので、ルール 3 をやぶってしまいます。ルール 3 をやぶらないようにするためにはハコ (3,3) に 1、ハコ (4,3) に 2 を入れるひつようがあります。
数字をはいちしましょう。
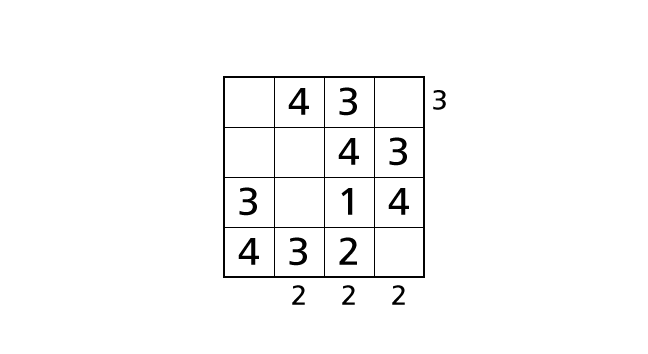
手順 9
3 行目と 4 行目に注目しましょう。ルール 1 より、それぞれの行には 1 から 4 の数字が 1 度ずつ出てくるので、ハコ (3,2) は 2 しか入れることができないハコ、ハコ (4,4) は 1 しか入れることができないハコ であることがわかります。
数字をはいちしましょう。
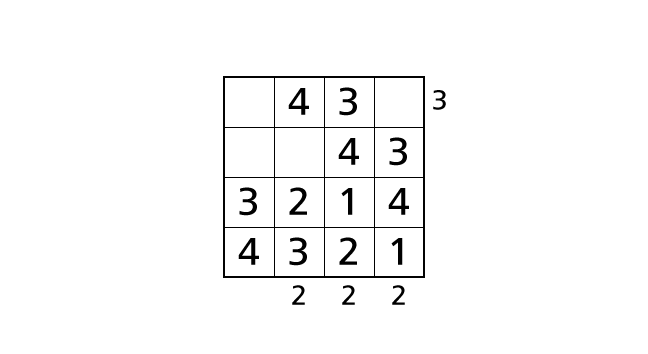
つぎは 2 列目と 4 列目に注目しましょう。ルール 2 より、それぞれの列には 1 から 4 の数字が 1 度ずつ出てくるので、ハコ (1,4) は 2 しか入れることができないハコ、ハコ (2,2) は 1 しか入れることができないハコ であることがわかります。
数字をはいちしましょう。
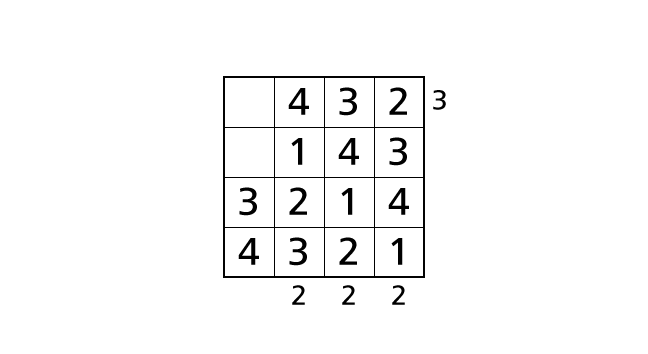
最後に 1 行目と 2 行目に注目しましょう。ルール 1 より、それぞれの行には 1 から 4 の数字が 1 度ずつ出てくるので、ハコ (1,1) は 1 しか入れることができないハコ、ハコ (2,1) は 2 しか入れることができないハコ であることがわかります。数字をはいちして完成です。

はじめてみよう
最新のビルディングパズルは ビルディングパズル で遊ぶことができます。
過去のビルディングパズルの問題は ビルディングパズル-アーカイブ からアクセスすることができます。
